To ask Unlimited Maths doubts download Doubtnut from https//googl/9WZjCW Find the domain and range of `1/sqrt(xx)` Misc 4 Find the domain and the range of the real function f defined by f (x) = √ ( (𝑥−1)) It is given that the function is a real function Hence, both its domain and range should be real numbers x can be a number greater 1 Here, f (x) is always positive, Minimum value of f (x) is 0, Maximum can be any value Hence, value of domain (x) should be atleast 1 and will go on till infinity Hence, Domain = 1,∞) Similarly, value of range How do you find Domain and the range of function f(x) = x1?

Find The Domain And The Range Of The Real Function F Defined By F X X 1 Brainly In
Draw the graph of f(x)= x-1 . find its domain and range
Draw the graph of f(x)= x-1 . find its domain and range-√(x1) √(3x) first determine the domain of the function For √ function, the input must be >=0, therefore x1>=0 => x>=1 and 3x>=0 => xArrow_forward Question View transcribed image text fullscreen Expand check_circle



What Is The Range Of The Function F X X 1 Quora
Find the domain and range of the function f(x)= 1/sqrt(xx) Share with your friends Share 14Domain is R {0} In order to find range, we may split the given function as two parts f (x) = (x 4)/ (x 4) f (x) = 1 if x > 4 f (x) = (x 4)/ (x 4) f (x) = 1 if x < 4 So, range is 1, 1 Apart from the stuff given above, if you need any other stuff in math, please use our google custom search hereQuestion 1 a) Find Domain and Range of the given function fx) 2w2 w6 b) Find (fogoh}x for f(x) = 2x² 1, g(x) = * and h(x) = out of This problem has been solved!
See the answer See the answer See the answer done loading urgnet required Show transcribed image text Expert Answer Stack Exchange network consists of 178 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers Visit Stack ExchangeThe range is simply y ≤ 2 The summary of domain and range is the following Example 4 Find the domain and range of the quadratic function y = x 2 4 x − 1 y = {x^2} 4x 1 y = x2 4x − 1 Just like our previous examples, a quadratic function will always have a domain of all x values
Find domain and range of f(x)= square root of (x 1)(3 x) Enter your answer for the domain using interval notation Set the radicand in greater than or equal to to find where the expression is defined Fx x 2 2 x 1 Solution to Example 3 Let fx4 on the square root of x 1 Identify the domain of the function fx x 3 Thank you very muchWrite the Domain and Range of the Function F ( X ) = X − 2 2 − X CBSE CBSE (Science) Class 11 Textbook Solutions Important Solutions 9 Question Bank Solutions 9938 Concept Notes & Videos 580 Syllabus Advertisement Remove all ads Write the Domain and Range of the Function F ( X ) = X − 2 2 − X Find the domain and range of the real function f(x) = x/1x^2 ━━━━━━━━━━━━━━━━━━━━━━━━━ ️Given real function is f(x) = x/1x^2 ️1 x^2 ≠ 0 ️x^2 ≠ 1 ️Domain x ∈ R ️Let f(x) = y ️y = x/1x^2 ️⇒ x = y(1 x^2) ️⇒ yx^2 – x y = 0 ️This is quadratic equation with real roots ️(1)^2 – 4(y)(y) ≥ 0




Find The Domain And Range Of The Function F R To R F X X 2 1




Find The Range Of I F X X 4 X 4 And Domain Of Ii F X 1 Log 10 1 X Sqrt X 2 Youtube
Algebra Q&A Library 1 find the domain and range of f(x) = 2 cos3x 1 find the domain and range of f(x) = 2 cos3x close Start your trial now!Find the domain of function f defined by Example 4 Find the range of function f defined by Solution to Example 4 The domain of this function is the set of all real numbers The range is the set of values that f(x) takes as x varies If x is a real number, x 2 is either positive or zeroAlgebra Find the Domain and Range f (x)=1/x f (x) = 1 x f ( x) = 1 x Set the denominator in 1 x 1 x equal to 0 0 to find where the expression is undefined x = 0 x = 0 The domain is all values of x x that make the expression defined Interval Notation




Interpretation Of Domain And Range Of A Function F Ppt Download




Example 15 F X 1 X What Is The Domain And Range Examples
5 4 3 2 1 c Solution for find the domain and range ƒx 1 x2 8 with GDC Let f x 2 cos 2 x 2sin 05 x for 0 x 3 where x is in radians A On the grid below sketch the curve of y f x indicating clearly the point P on the curve where the function has a max or min valueInformally, if a function is defined on some set, then we call that set the domain The values taken by the function are collectively referred to as the range For example, the function takes the reals (domain) to the nonnegative reals (range) The sine function takes the reals (domain) to the closed interval (range) (Both of these functions can be extended so that their domains are theSOLUTION find the range and domain f (x)=1/x2 Question find the range and domain You can put this solution on YOUR website!




Misc 5 Find Domain And Range Of F X X 1 Class 11




Find Domain And Range Of F X Square Root Of X 1 3 X Maths Relations And Functions Meritnation Com
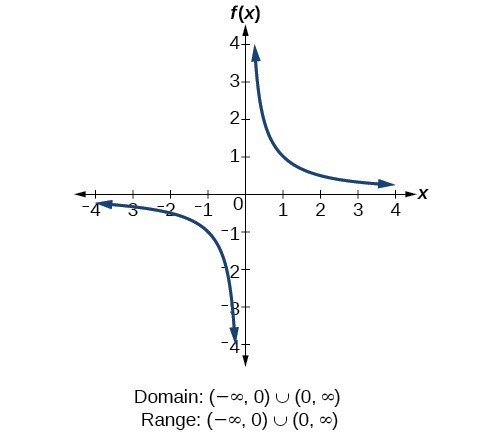
Figure 3 Domain and range of a function and its inverse When a function has no inverse function, it is possible to create a new function where that new function on a limited domain does have an inverse function For example, the inverse of f ( x) = x \displaystyle f\left (x\right)=\sqrt {x} f (xThe domain and range of the function f= ((1/1x2)) x ∈ R, x ≠ ± 1 are respectively (A) R 1, 1 (∞, 0) ∪ 1, ∞) (B) R, (∞, 0) ∪ 1 Tardigrade Pricing Domain of fx xx21 Use the distributive property to multiply f 1x by x2 X 1 x 1 The range is also all real numbers except zero 4 Points If Fx 3x2 1 X 2 1x1 X 22 b Find The Domain And The Range Of F Multiply both sides of the equation by x2 1 x 2 0 Y sqrt x1x Call this f1 x




How To Find Domain And Range From A Graph Video Khan Academy
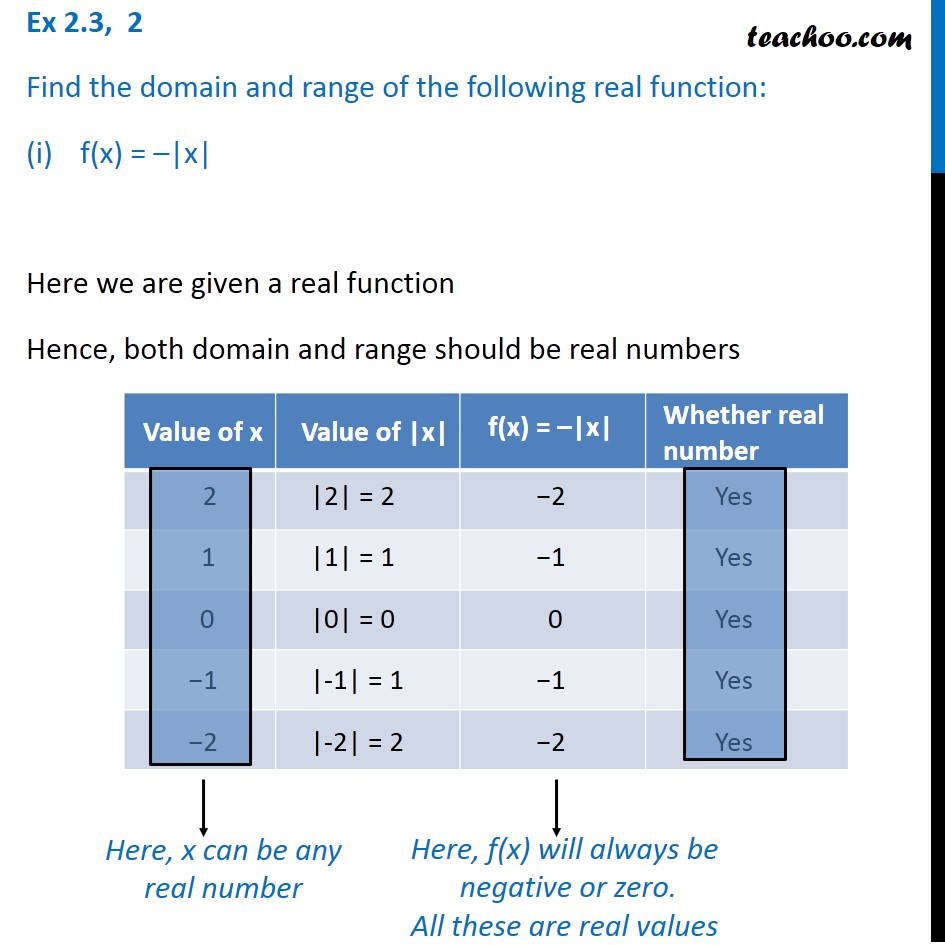



Ex 2 3 2 Find Domain And Range I F X X Chapter 2
Stack Exchange network consists of 177 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers Visit Stack ExchangeFree functions domain calculator find functions domain stepbystep This website uses cookies to ensure you get the best experience By using this website, you agree to our Cookie Policy Arithmetic Mean Geometric Mean Quadratic Mean Median Mode Order Minimum Maximum Probability MidRange Range Standard Deviation Variance Lower QuartileHow would you specify that the range of a function consists of 2 values, but no other values?




Tutorial Function Domain And Range Pdf Variable Mathematics Domain Of A Function




Find Domain And Range Of Real Functions 1 F X X 2 3 X 2 F X 1 Sqrt X 5 3 F X X 1 X 2
Find the domain and range of the function `f(x)=(1)/sqrt(x5)` f (x) = 1/√x−5 Now for real value of x5≠0 and x5>0 ⇒ x≠5 and x>5 Hence the domain of f = (5, ∞) And the range of a function consists of all the second elements of all the ordered pairs, ie, f(x), so we have to find the values of f(x) to get the required range Now we know for this function x5>0 taking square root on bothQuestion Given the functions f (x) = square root x, and g (x) = (x 5) / (2x 1), find the domain and range of fg (x) composite function Answer domain of fg (x) composite function x is an element of R, x < 05, x is greater or equal to 5 Answer range of fg (x) composite function fg (x) is an element of R, fg (x) is between 0 and




Ex 2 2 6 Determine Domain And Range Of R X X 5



Q Tbn And9gcrbtq2n2wyqxjku7shcld Gzp Crxxctbrkotgywsn Sp4ftbet Usqp Cau
Domain {xl x≠0} Range 1,1 or just 1 and 1, In f(x), all y values are either 1 or 1 The range contains no verticle y values greater than or less than 1 and 1 So maybe I should write this range as {yl y = 1 and 1} or 1U1? The range is the set of all valid values Find the domain and range of f (x)=x2/1x2 Domain of the function is where the function is defined The given function X R Let fx y y x1x2 x y1 x2 yx2 x y 0 This is quadratic equation with real roots Find the domain and range ƒx 1 x2 Maintain the following steps 1When the given function is of the form f(x) = 2x 5 of f(x) = x 2 – 2, the domain will be "the set of all real numbers When the given function is of the form f(x) = 1/(x – 1), the domain will be the set of all real numbers except 1 In some cases, the interval be specified along with the function such as f(x) = 3x 4, 2 < x < 12




Find The Domain And The Range Of The Real Function F Defined By F X X 1 Brainly In
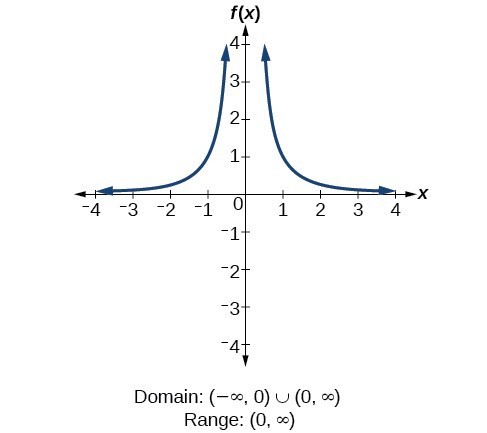



Determine Domain And Range From A Graph College Algebra
Solution for 1 find the domain and range of f(x) 2 cos3xAnswer and Explanation 1 Given f(x) = 1 x f ( x) = 1 x Domain Since the function is a fraction, the value of the variable are all real numbers except 0 0 since it will result to an undefined 2x 1 = 0 2x = 1 x = 1 / 2 Therefore , Domain = R { 1/2 } All real numbers are used as range here For getting solve the denominator of the given fraction and reduce the value of x from the real number "R" Hope it helps you dude




Find The Domain And Range Of The Function F X 1 2 Sin3x Youtube




Domain And Range Of F X X 3 X 3 Are Respectively
Answer to Consider F(x, y) = 1/(x^2 y^2) Find the domain, the range, and the x and y intercepts By signing up, you'll get thousands of (a) Show that f is onetoone (b) To find (f 1) ' (a) (c) Calculate f 1 (x) and state the domain and range of f 1 (d) Calculate (f 1) ' (a) from the formula in part (c) and check that it agrees with the result of part (b) (e) Sketch the graphs of f and f 1 on the same axes f (x) = xWere given a function and we're asked to find the domain and range of dysfunction Function is F of X equals one plus X square Notice that the function F is a polynomial function that's a quadratic function and therefore the domain of F is all real numbers



1




Given F X X 1c2x 8 G X 2x 8cx 1 And H X F X G X Then Which Of The Following Holds
Algebra Find the Domain and Range f (x)=1/ (x1) f (x) = 1 x − 1 f ( x) = 1 x 1 Set the denominator in 1 x−1 1 x 1 equal to 0 0 to find where the expression is undefined x−1 = 0 x 1 = 0 Add 1 1 to both sides of the equation x = 1 x = 1 The domain is all values of xExample 1 Find the domain and range of the function y = 3 x 2 Graph the function on a coordinate plane The graph is nothing but the graph y = 3 x translated 2 units to the left The function is defined for all real numbers So, the domain of the function is set of real numbersSo, Domain (f) = x ∈ R Range of ( f ) We know that ∣ x ∣ is always positive So, if a positive quantity is being subtracted from 1 then for all other values of ∣ x − 2 ∣ except 0 , 1 y will be negative and maximum value will be when ∣ x − 2 ∣ = 0 then y = 1




Find The Domain And Range Of The Function F X 16 X 2 Donimain




Find The Range Of I F X X 4 X 4 And Domain Of Ii F X 1 Log 10 1 X Sqrt X 2
Rule The domain of a function on a graph is the set of all possible values of x on the xaxis For domain, we have to find where the x value starts and where the x value ends ie, the part of xaxis where f(x) is definedFirst week only $499!Answer f (x) = x−5 For f (x) to be defined, the term under the Squareroot should be greater than or equal to zero x−5 ≥0 x ≥ 5 So, the domain is 5,∞)
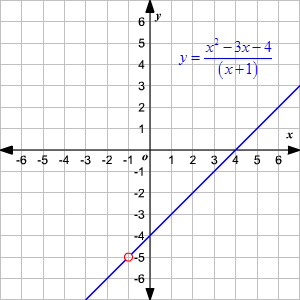



Domain And Range Of Rational Functions




Find The Domain And Range Of The Function F X Y Chegg Com
Find domain and range from graphs Another way to identify the domain and range of functions is by using graphs Because the domain refers to the set of possible input values, the domain of a graph consists of all the input values shown on the x axis The range is the set of possible output values, which are shown on the y axisSet the denominator equal to zero Remember, dividing by 0 is undefined So if we find values of x that make the denominator zero, then we must exclude them from the domain Now to find the range, notice thatThe domain is all real numbers, and the range is all real numbers f(x) such that f(x) ≤ 4 You can check that the vertex is indeed at (1, 4) Since a quadratic function has two mirror image halves, the line of reflection has to be in the middle of two points with the same y value




Find The Domain And Range Of Following Function F X 1 Root X Mod X Brainly In




Find The Domain And The Range Of The Real Function F Defined By F X X 1
Best answer Given that f (x) = 1/√ (x 5) Here, it is clear that (x) is real when x – 5 > 0 ⇒ x > 5 Hence, the domain = (5, ∞) Now to find the range put For x ∈ (5, ∞), y ∈ R Hence, the range of f = R Please log in or register to add a commentSo, the domain of the function f(x) is (∞,∞) Now to find the range, say f(x)= y, which gives x²9=y² or, x= ±√(y²9) Since x is a real number, y²9 must be positive or, y²>9 which gives y ∈ (3,∞),since y>0, which is the required range of f(x)Clearly f(x) = x 1 is defined for all real x, therefore domain of f = D(f) = R (the set of real numbers) Further as f(x) >/= 0 for all x € D(f) = R ,therefore range of f = set of all non negative real numbers




How To Find The Domain And Range Of A Function 14 Steps




Find The Domain And Range Of F X 9 X 2 Brainly In
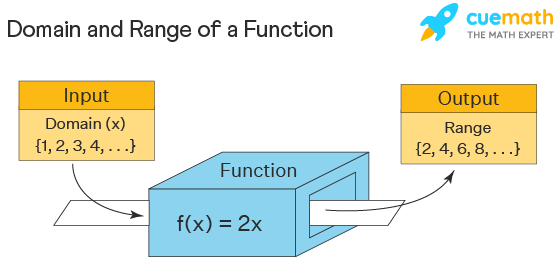
Domain and range The domain and range of a function is all the possible values of the independent variable, x, for which y is defined The range of a function is all the possible values of the dependent variable y The example below shows two different ways that a function can be represented as a function table, and as a set of coordinates




Find Domain And Range Of Function F X 1 3cos2x Maths Relations And Functions Meritnation Com




Find Domain And Range Of 1 9 X 2 Dumians
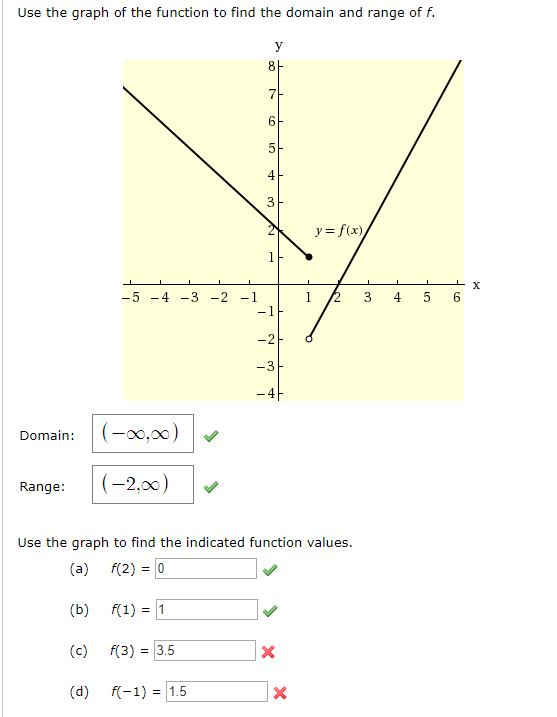



Use The Graph Of The Function To Find The Domain And Chegg Com




Hence The Range Is Illustration 1 10 Find The Domain And Range Of F X Vx2



Domain And Range Examples Domain And Range Of Functions




9 Find The Domain And Range Of F 1 Where F X X 1 Chegg Com




Find The Domain And Range Of The Function F X 1 Sqrt X 5 Youtube




Find The Domain Or Range Of Following Function Tex F X Sqrt X 1 3 X Tex Brainly In



Find The Domain And Range Of The Real Function F X X 2 9 Sarthaks Econnect Largest Online Education Community




Find Domain And Range Of Real Functions 1 F X X 2 3 X 2 F X 1 Sqrt X 5 Youtube




Find The Domain And Range Of The Following Real Functions Quest




Find Domain And Range Of F X 1 2 Sin3x Maths Relations And Functions Meritnation Com




How To Find Domain And Range Of The Inverse Of A Relation Sat Math



Hello Sir I Need A Full Explanation Of This Sum Find Domain And Range Of F X 2x 3 3 Mathematics Topperlearning Com 4fb8db22



Determine Domain And Range From A Graph College Algebra




Answered 3x For 1 X 1 Let F X X 4 For Bartleby




Find Domain And Range Of Real Function F Defined By F X X 1 Maths Relations And Functions Meritnation Com




Find Domain And Range Of Function Y 1 X Youtube




Find The Range Of Each Of The Following Functions F X X 3 F X 1 X 2 F X X 4 Youtube



What Is The Range Of The Function F X X 1 Quora




Find The Domain The Range Of Each Of The Following Function F X 1 Sqrt 4 3sinx




Find The Domain And Range Of The Function F X X X 1 X 1 Maths Relations And Functions Meritnation Com



Find Domain And Range Of Function Y 1 X Youtube




Misc 6 Let F X X2 1 X2 X R Find Range Chapter 2




The Problem Was To Graph The Function Find The Chegg Com




Find The Domain And The Range Of The Real Function Defined By F X Sqrt X 1
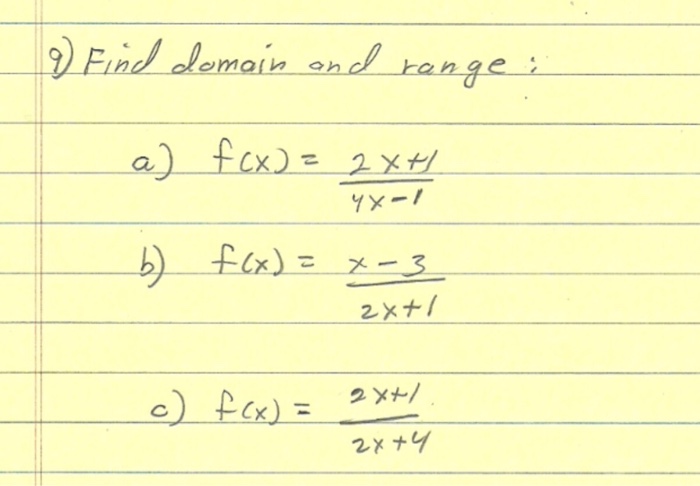



Find Domain And Range F X 2x 1 4x 1 F X Chegg Com




Find The Domain And Range Of The Function F X 1 1 X 2 X In R X 1 Dot Youtube




Q 1 A Sm Find The Domain And Range Of Each Chegg Com




Find The Domain And Range Of F X 1 Sin X Find Chegg Com
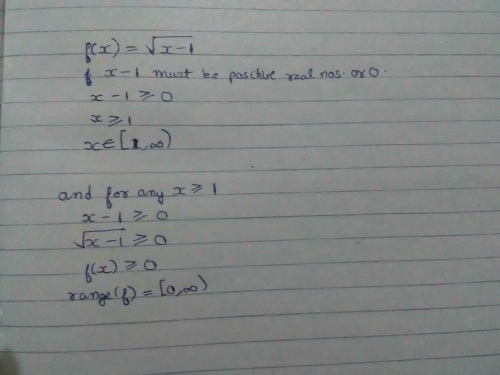



Find The Domain And Range Of Real Function F Defined By F X Underoot Of X 1 Edurev Class 11 Question



What Is The Range Of The Function F X X 1 Quora



Find The Domain And The Range Of The Real Function F Defined By F X Sqrt X 1 Sarthaks Econnect Largest Online Education Community



What Is The Domain And Range Of Y E X Socratic




Find The Domain And The Range Of The Real Function F X 1 X 3




Find The Domain And Range Of The Function F X 1 5 X Brainly In




Find Domain And Range Of 1 F X X 1 2x 1 Ese Krvaya Mam Ne Lekin Smjh Mei Nhi Ay K Ese Kyu Kiy Brainly In




Exercise 1 3 Functions Problem Questions With Answer Solution




Find Domain And Range Of Sine Inverse 5x 1 Youtube




Domain And Range Of 1 X 2 2x 8 Youtube




F X 3x 2x 8 Find Domain And Range Brainly In




Find Domain And Range Of F X 1 16 X 2 Brainly In




Find The Domain And Range Of F X Root Of X 1 Brainly In
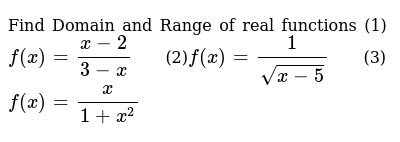



Find Domain And Range Of Real Functions 1 F X X 2 3 X 2 F X 1 Sqrt X 5 3 F X X 1 X 2




How To Find The Domain And Range Of A Function 14 Steps



Q Tbn And9gcqj529kunx E23asbmwgf8sdjnucswezuevva8edino5czgfbjv Usqp Cau




F X 1 X 2 1 Find Domain And Range Of The Following Function Brainly In
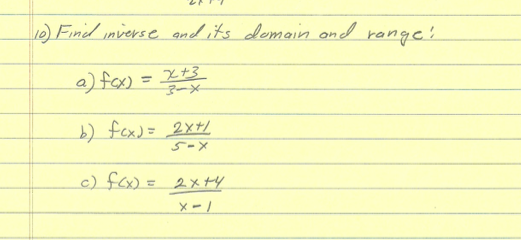



Find Inverse And Its Domain And Range F X X Chegg Com




Rd Sharma Solutions For Class 11 Maths Updated For 21 22 Chapter 3 Functions




Find The Domain And Range Of The Function F X 1 1 X 2 X In R X 1 Dot




F X X X 1 Find Domain And Range Plzz Experts Answer Fast My Exam Is Tomorrow Maths Relations And Functions Meritnation Com




Given That F X 1 2x 3 Find F 1 The Domain Of Chegg Com




Domain And Range Calculator Wolfram Alpha




Domain And Range Of Quadratic Functions Video Khan Academy



What Is The Range Of The Function F X X 1 Quora



What Is The Range Of The Function F X X 1 Quora




Find The Domain And Range Of The Function Defined By F X 1 9 X Please Help Me Brainly In




Example 15 F X 1 X What Is The Domain And Range Examples




Find Domain And Range F X X 1 X 1 Maths Relations And Functions Meritnation Com




Misc 4 Find Domain And Range Of F X Root X 1 Chapter 2




6 Ways To Find The Domain Of A Function Wikihow
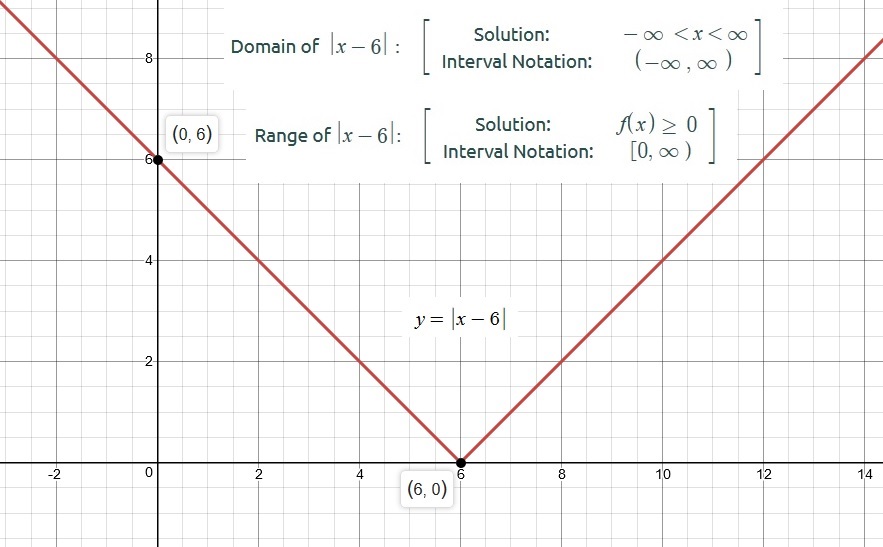



How Do You Find The Domain And Range Of Y X 6 Socratic




Misc 4 Find Domain And Range Of F X Root X 1 Chapter 2




5 Given Function F X 3x 1 Find A Domain And Chegg Com



What Is The Domain And Range Of X 2 1 X 2 Quora



What Is The Range Of 1 X 2 1 Quora




Find The Domain And Range Of The Function F X Sin 1 1 E X 1




If F X X 2 X X 2 2x Then Find The Domain And Range Of F Show That F Is One One Youtube
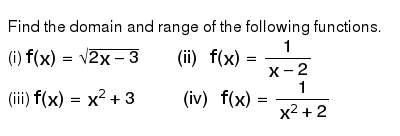



Find The Domain And Range Of The Following Functions I F X Sqrt 2x 3 Ii F X 1 X 2 Iii F X X 2 3 Iv F X 1 X 2 2
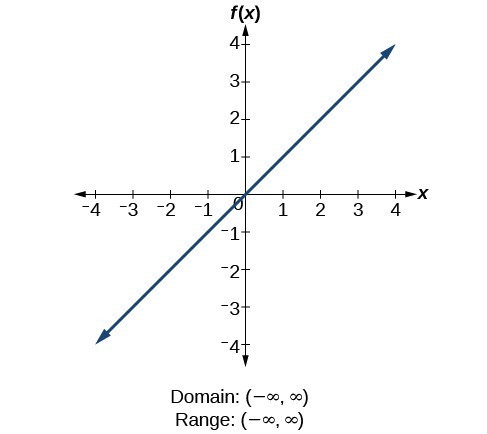



Find Domains And Ranges Of The Toolkit Functions Math 1314 College Algebra




Find The Domain And Range Of The Function F X 1 1 X 2 X In R X 1 Dot Youtube



How Do You Find The Domain And Range Of Y Sqrt 3x 5 Socratic




Find The Domain And Range Of The Inverse Of The Given Chegg Com




Find Domain And Range Of F X X 1 X 2



Find The Domain And Range Of The Following Real Functions I F X X Ii F X 9 X 2 Sarthaks Econnect Largest Online Education Community




Find The Domain And Range Of The Function F X Chegg Com




Find The Domain And Range Of F X X 1 Youtube



3



0 件のコメント:
コメントを投稿